Học cách giải hệ phương trình là nội dung quan trọng trong Toán lớp 9 và thường xuất hiện ở nhiều bài thi cũng như các lớp khóa trên. Bài viết sau tổng hợp 3 phương pháp là pp thế, pp cộng đại số và pp giải bằng máy tính cùng với đó là những dạng bài tập thường gặp. Ta bắt đầu tìm hiểu ngay!
Các phương pháp giải hệ phương trình
Phương pháp thế
Phương pháp thế là một trong những cách biến đổi tương đương một hệ phương trình, ta sử dụng quy tắc thế, bao gồm hai bước, sau đây:
- Bước 1: Từ phương trình thứ nhất của hệ, biểu diễn một ẩn theo ẩn kia và thế vào phương trình thứ hai để có phương trình mới chỉ chứa một ẩn.
- Bước 2: Thay phương trình thứ hai bằng phương trình mới trong hệ, giữ nguyên phương trình thứ nhất, ta được hệ phương trình mới tương đương với hệ đã cho.
Chú ý: Nếu thấy xuất hiện phương trình có các hệ số của hai ẩn đểu bằng 0 thì hệ phương trình đã cho có thể có vô số nghiệm hoặc vô nghiệm.
Các dạng toán thường gặp
Dạng 1: Giải hệ phương trình bằng phương pháp thế
Phương pháp: Căn cứ vào quy tắc thế, để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế, ta làm như sau:
Bước 1. Rút $x$ hoặc $y$ từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta được phương trình mới chỉ còn một ẩn.
Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.
Để lời giải được đơn giản, ta thường chọn phương trình có các hệ số có giá trị tuyệt đối không quá lớn (thường là $1$ hoặc$ – 1$ ) và rút $x$ hoặc $y$ có hệ số có giá trị tuyệt đối nhỏ hơn qua ẩn còn lại.
Dạng 2: Giải hệ phương trình quy về hệ phương trình bậc nhất hai ẩn
Phương pháp:
Bước 1. Biến đổi hệ phương trình đã cho về hệ phương trình bậc nhất hai ẩn.
Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế như ở Dạng 1.
Dạng 3: Giải hệ phương trình bằng cách đặt ẩn phụ
Phương pháp:
Bước 1. Đặt ẩn phụ cho các biểu thức chung trong các phương trình của hệ phương trình đã cho để thu được hệ phương trình bậc nhất hai ẩn mới.
Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế như ở Dạng 1, ta tìm được nghiệm của hệ phương trình đã cho.
Dạng 4: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước.
Phương pháp:
Một số kiến thức thường sử dụng
- Hệ phương trình bậc nhất hai ẩn $\left\{ \begin{array}{l}ax + by = c\\a’x + b’y = c’\end{array} \right.$có nghiệm $\left( {{x_0};{y_0}} \right) \Leftrightarrow \left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c’\end{array} \right..$
- Đường thẳng $d:ax + by = c$đi qua điểm$M\left( {{x_0};{y_0}} \right)$$ \Leftrightarrow a{x_0} + b{y_0} = c.$
Ví dụ 1: hãy giải hệ phương trình sau \(\left\{\begin{matrix} x – y =3 & & \\ 3x-4y=2 & & \end{matrix}\right.\)
Giải
Rút \(x\) từ phương trình trên rồi thế vào phương trình dưới , ta được:

Vậy hệ đã cho có nghiệm là \((x;y)=(10; 7)\).
Ví dụ 2: \(\left\{\begin{matrix} 7x – 3y =5 & & \\ 4x+y=2 & & \end{matrix}\right.\)
Giải
Rút \(y\) từ phương trình dưới rồi thế vào phương trình trên, ta có:
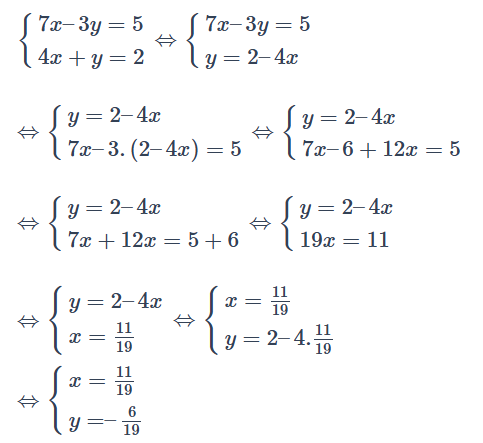
Vậy hệ có nghiệm duy nhất là \({\left(\frac{11}{19}; \frac{-6}{19} \right)}\)
Phương pháp cộng đại số
Để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số, ta sử dụng phương pháp cộng đại số , bao gồm hai bước sau đây :
Bước 1: Cộng hoặc trừ từng vế của hai phương trình trong hệ để được phương trình mới.
Bước 2: Thay phương trình mới vào một trong hai phương trình của hệ, giữ nguyên phương trình còn lại, ta có hệ mới tương đương với hệ đã cho.
Các dạng toán thường gặp
Dạng 1: Giải hệ phương trình bằng phương pháp cộng đại số
Từ quy tắc cộng đại số, để giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số ta làm như sau:
Bước 1. Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trog hai phương trình bằng nhau hoặc đối nhau.
Bước 2. Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để thu được một phương trình mới (chỉ còn một ẩn ).
Bước 3. Giải phương trình một ẩn vừa thu được từ đó suy ra nghiệm của hệ phương trình đã cho .
Dạng 2: Giải hệ phương trình đưa về hệ phương trình bậc nhất hai ẩn
Bước 1. Biến đổi hệ phương trình đẫ cho về hệ phương trình bậc nhất hai ẩn .
Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số như ở dạng $1$ .
Dạng 3: Giải hệ phương trình bằng phương pháp đặt ẩn phụ
Bước 1. Đặt ẩn phụ cho các biểu thức chung có trong các phương trình của hệ phương trình đã cho để được hệ phương trình bậc nhất hai ẩn mới.
Bước 2. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số như ở dạng $1$
Bước 3. Trả lại biến đã đặt từ đó tìm được nghiệm của hệ phương trình đã cho.
Dạng 4: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước
Ta thường sử dụng các kiến thức:
+ Hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}ax + by = c\\a’x + b’y = c’\end{array} \right.\)
có nghiệm \(({x_0};{y_0})\) \( \Leftrightarrow \left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c’\end{array} \right..\)
+ Đường thẳng \(d:ax + by = c\) đi qua điểm \(M({x_0};{y_0})\, \Leftrightarrow a{x_0} + b{y_0} = c.\)
Ví dụ 1: Hãy giải hệ pt sau \(\left\{\begin{matrix} -5x + 2y = 4 & & \\ 6x – 3y =-7 & & \end{matrix}\right.\)
Giải
Nhân phương trình trên với \(3\), nhân phương trình dưới với \(2\), rồi cộng vế với vế của hai phương trình trong hệ, ta được:
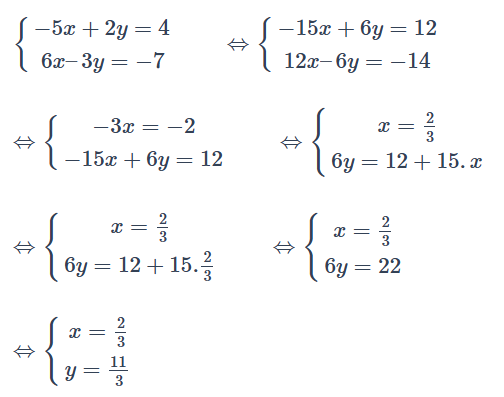
Vậy hệ đã cho có nghiệm duy nhất là \({\left(\frac{2}{3}; \frac{11}{3} \right)}\)
Ví dụ 2: Hãy giải hệ phương trình: \(\left\{\begin{matrix} 3x – 2y = 10& & \\ x – \frac{2}{3}y = 3\frac{1}{3} & & \end{matrix}\right.\)
Giải
Đổi hỗn số về phân số rồi nhân hai vế của phương trình dưới với \(3\) sau đó trừ vế với vế của hai phương trình ta được:
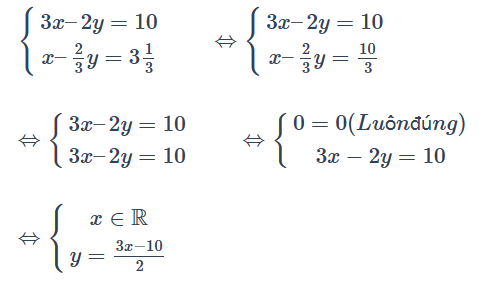
Vậy hệ phương trình có vô số nghiệm.
Ví dụ 3: Hãy giải hpt sau: \(\left\{\begin{matrix} \frac{1}{x} – \frac{1}{y} = 1& & \\ \frac{3}{x} + \frac{4}{y} = 5& & \end{matrix}\right.\)
Giải
Điền kiện \(x ≠ 0, y ≠ 0\).
Đặt \(\left\{\begin{matrix} u = \frac{1}{x} & & \\ v = \frac{1}{y} & & \end{matrix}\right.\) (với \(u \ne 0,\ v \ne 0\) ).
Hệ phương trình đã cho trở thành:
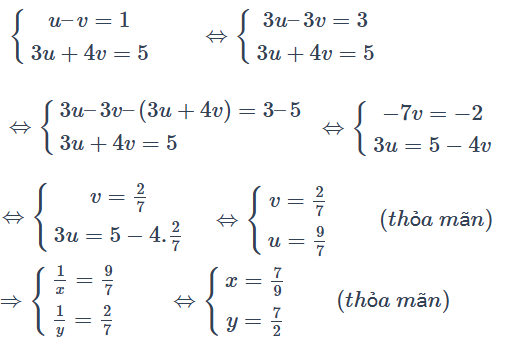
Vậy hệ đã cho có nghiệm duy nhất \( {\left(\frac{7}{9};\frac{7}{2} \right)}\).
Sử dụng máy tính cầm tay
Để tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay, cần sử dụng loại máy có chức năng này (thường có phím MODE). Đầu tiên, viết hệ phương trình dưới dạng: $\left\{ \begin{array}{l} {a_1}x + {b_1}y = {c_1}\\ {a_2}x + {b_2}y = {c_2} \end{array} \right.$
Ví dụ: Chẳng hạn để tìm nghiệm của hệ ta viết dưới dạng $\left\{ \begin{array}{l} 2x + 3y – 4 = 0\\ 5x + 6y – 7 = 0 \end{array} \right.$
Ta sẽ viết lại hệ: $\left\{ \begin{array}{l} 2x + 3y = 4\\ 5x + 6y = 7 \end{array} \right.$
Lúc này ta bấm máy tính như sau
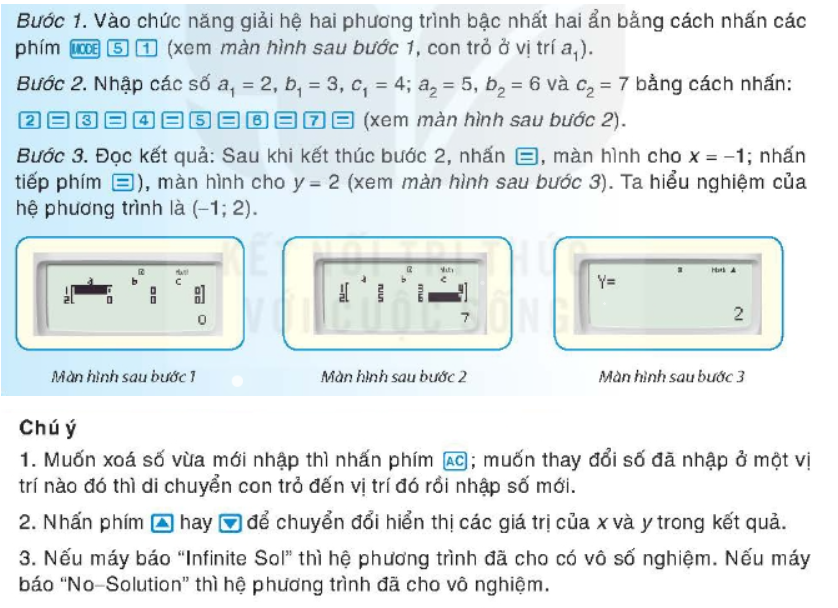
Ví dụ: Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình: $\left\{ \begin{array}{l} 2x + y = 10\\ – y = 2 – x \end{array} \right.$
Giải
Đầu tiên ta phải phải chuyển nó về dạng của máy có dạng như sau $\left\{ \begin{array}{l} 2x + y = 10\\ x – y = 2 \end{array} \right.$

Máy hiện ra kết quả $\left\{ \begin{array}{l} x = 4\\ y = 2 \end{array} \right.$
Bài tập
Bài tập có lời giải
Bài tập tự luyện
Bài tập 1: Dùng phương pháp thế để giải các hệ pt sau:
a) \(\left\{ \begin{array}{l}7x + y = 19\\x + 7y = – 11\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x – 6y = – 3\\5x + 8y = 7\end{array} \right.\)
c) \(\left\{ \begin{array}{l}x – 2y = 1\\ – 2x + 4y = – 2\end{array} \right.\)
Bài tập 2: Dùng phương pháp cộng đại số để giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x – 5y = 8\\2x – 7y = 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}4x + 3y = 6\\2x + y = 4\end{array} \right.\)
c) \(\left\{ \begin{array}{l}0,3x + 0,5y = 3\\1,5x – 2y = 1,5\end{array} \right.\)
Bài tập 3. Sử dụng máy tính cầm tay thích hợp, tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}9x – 5y = – 11\\22x + 17y = 3;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}\frac{2}{5}x – \frac{3}{8}y = \frac{1}{4}\\ – \frac{4}{5}x + \frac{9}{8}y = \frac{7}{8}\end{array} \right.\)
c) \(\left\{ \begin{array}{l}0,6x – 0,7y = 1,5\\ – 0,2x + 0,3y = – 1\end{array} \right.\)
Bài tập 4: Hãy giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x – y} \right) = 4\\\left( {x + y} \right) + 2\left( {x – y} \right) = 5\end{array} \right.\)
b) \(\left\{ \begin{array}{l}3\left( {x + 2y} \right) – 4\left( {2x – y} \right) = 5\\4\left( {x + 2y} \right) + 3\left( {2x – y} \right) = 15\end{array} \right.\)
c) \(\left\{ \begin{array}{l}11x – 13y = – 7\\7x + 19y = 2\end{array} \right.\)
d) \(\left\{ \begin{array}{l}\frac{1}{8}x + \frac{3}{4}y = \frac{1}{{16}}\\ – \frac{4}{5}x + \frac{7}{5}y = \frac{1}{5}\end{array} \right.\)
e) \(\left\{ \begin{array}{l}0,12x – 0,15y = – 2,4\\0,21x + 0,35y = – 3,6\end{array} \right.\)
Bài tập 5: Xác định \(a\) và \(b\) để đồ thị của hàm số \(y = ax + b\) đi qua hai điểm \(A\) và \(B\) trong mỗi trường hợp sau:
a) \(A\left( {3; – 2} \right)\) và \(B\left( { – 3;1} \right)\)
b) \(A\left( {0;2} \right)\) và \(B\left( {\sqrt 3 ;2} \right)\)